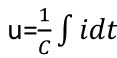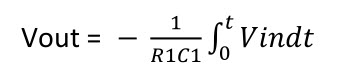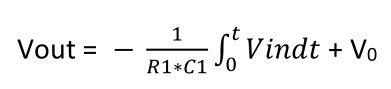积分运算放大器是由反相运算放大电路改造(将反馈电阻Rf替换成电容)而成,产生的输出电压幅度与输入信号的电压幅度和持续时间有关,即输出信号的大小取决于输入端电压保持的时间长度,因为通过电容器发生的负反馈,实际就是通过反馈回路的电流对电容器充电或放电,从而实现波形的变换。
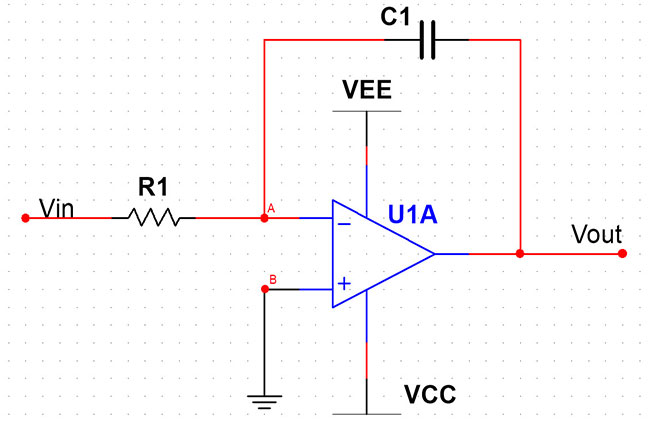
积分运算电路分析
图中Rin = R1, Cf = C1
由电容极板间的电压值定义
U=Q/C,
和极板间电流和电压的关系
i = dq/dt = C(du/dt) ,
则 ,
du/dt = dq/Cdt = (1/C)*(dq/dt)
对上式积分得
,可知,电容两端的电压值与流过电容的电流成积分关系
由理想运放的“虚短”得
uA = uB = 0(虚短,接地) 则Vout = -VC1
对于电容的电流iC1 用电容电流定义式
iC1 = dq/dt = C(du/dt) = C *(dVout/dt)
又由理想运放的“虚断”得
iin =iR1 = iC1=Vin/R1= ,
进一步化简得
Vin/Vout * [dt/(R1*C1)] = 1,
对上式在时间上积分
式中电阻与电容的乘积称为积分时间常数,通常用符号τ表示,即
τ=RC
如果在开始积分之前,电容两端已经存在一个初始电压,则积分电路将有一个初始的输出电压Uo(0),此时
积分运算放大电路的扩展
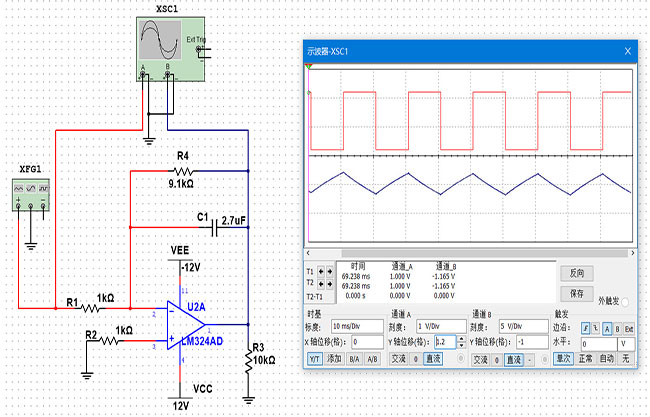
下面的仿真电路在前面分析的标准积分运算电路中加入了反馈电阻R4, (R2是一个平衡电阻,可以根据实际情况进行取舍)
电阻R4与一个连续充电和放电的电容器并联。在电容器C1两端添加此反馈电阻器R4使电路具有有限闭环电压增益的反相放大器的特性,增益为R4/R1。
针对直流信号和交流信号的增益表达式
直流电压增益Av = -R4/R1
交流电压增益Av = -(R4/R1) * [1/(1 + 2πfCR4)],
角频率f0 = 1/(2πCR4)