将积分运算放大电路的输入电阻和反馈回路的电容互换就构成了微分运算放大电路,微分器运算电路产生的输出信号是输入信号的一阶导数,更清晰的描述是微分运算放大电路产生与输入电压相对于时间的变化率成正比的输出电压,输入电压信号的变化越快或越大,输入电流越大,响应的输出电压变化就越大,变得更像“尖峰”形状。
微分运算电路分析
从微分电路的输入端结构可以看出,输入信号经过输入电容C进入运放输入端,所以微分电路对低频信号具有非常高的容抗XC(XC=1/2πfc),导致增益小;对高频输入信号则可以获得更高的电压增益(Rf/XC),但是高频输入信号会使微分运算放大电路变得不稳定并发生振荡。这主要是由于一阶效应,它决定了运算放大器电路的频率响应,导致二阶响应,在高频下输出电压远高于预期。为避免这种情况,需要通过在反馈电阻器Rf两端添加一个额外的小值电容器来降低电路的高频增益。
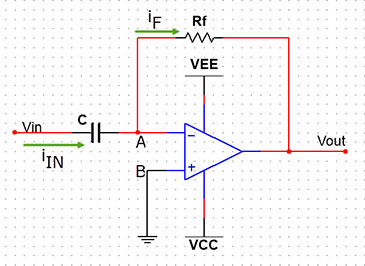
由理想运放的虚断路,得
iIN = iF,则iF = -Vout/Rf
由电容器上的电荷Q,电容C和电容器两端的电压V之间的关系
Q = C * V
得流过电容的电荷变化率
dQ/dt = C * dVin/dt
而电容的电荷变化率在电路中表现为电流,即
iIN = C * dVin/dt
对上面各式进行输入输出形式的化简得
Vout = - Rf * C* dVin/dt
由上式可知,输出电压Vout是常数–Rf *C乘以输入电压Vin对时间的导数。
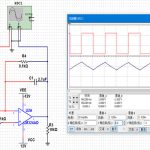
微分电路仿真
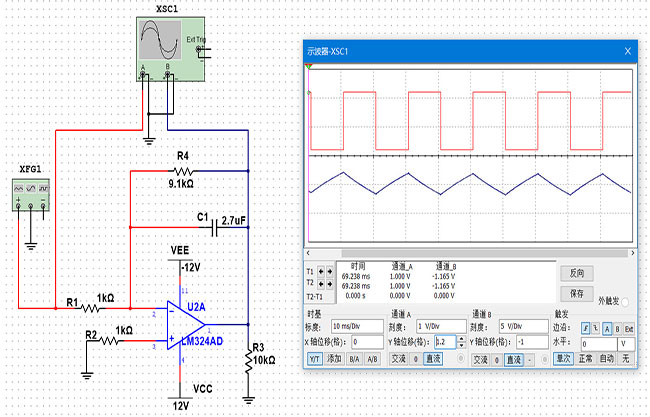
输入方波输出尖峰波
输入三角波输出方波
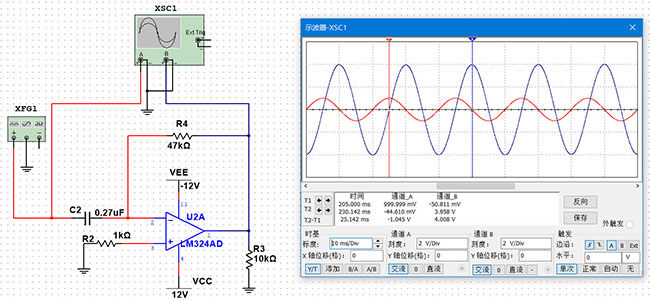
输入正弦波输出余弦波
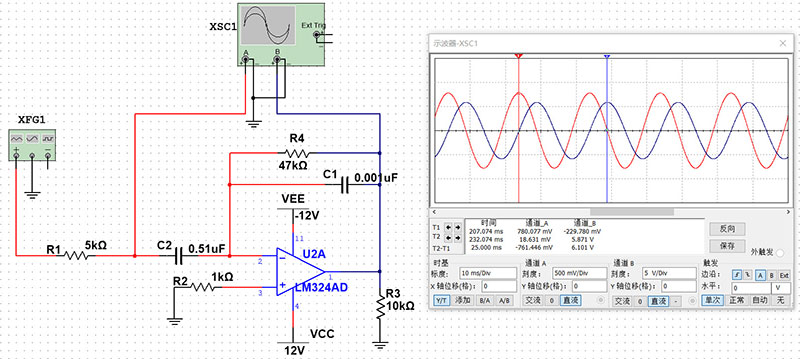
改进型运算微分放大电路
输入电阻器RIN以Rƒ/RIN的比率限制微分器的增益增加该电路现在在低频下充当微分器放大器,在高频下充当具有电阻反馈的放大器,从而提供更好的噪声抑制。
通过将电容器C1与微分器反馈电阻器R4并联连接,可实现更高频率的额外衰减。